Ada tiga langkah dalam induksi matematika yang diperlukan untuk membuktikan suatu rumus atau pernyataan. Langkah-langkah tersebut adalah :
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = 1.
- Mengasumsikan bahwa rumus atau pernyataan tersebut benar untuk n = k.
- Membuktikan bahwa rumus atau pernyataan tersebut benar untuk n = k + 1.
Untuk menerapkan induksi matematika, kita harus bisa menyatakan pernyataan P (k + 1) ke dalam pernyataan P(k) yang diberikan. Untuk meyatakan persamaan P (k + 1), substitusikan kuantitas k + 1 kedalam pernyataan P(k).
Jenis Induksi Matematika
- Deret Bilangan
Sebagai ilustrasi dibuktikan secara induksi matematika bahwa  .
.
untuk n = 1, maka :
1 = 1
Bentuk untuk n = 1 rumus tersebut benar.
Misal rumus benar untuk n = k, maka:
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Sehingga:
Pembuktiannya:
 (dalam langkah 2, kedua ruas
(dalam langkah 2, kedua ruas
ditambah k + 1)
![= \frac{1}{2}k (k + 1) +\frac{1}{2} [2(k + 1)] = \frac{1}{2}k (k + 1) +\frac{1}{2} [2(k + 1)]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) . (k + 1) dimodifikasi menyerupai
. (k + 1) dimodifikasi menyerupai  )
)
![= \frac{1}{2}[k(k + 1) + 2(k + 1)] = \frac{1}{2}[k(k + 1) + 2(k + 1)]](data:image/gif;base64,R0lGODlhAQABAIAAAAAAAP///yH5BAEAAAAALAAAAAABAAEAAAIBRAA7) (penyederhanaan)
(penyederhanaan)
 (terbukti)
(terbukti)
- Bilangan bulat hasil pembagian
Suatu bilangan dikatakan habis dibagi jika hasil pembagian tersebut adalah bilangan bulat. Sebagai ilustrasi, dibuktikan secara induksi matematika bahwa  habis dibagi 9.
habis dibagi 9.
untuk n = 1, maka:
= 27
27 habis dibagi 9, maka n = 1 benar.
Misal rumus benar untuk n = k, maka :
 (habis dibagi 9)
(habis dibagi 9)
 (b merupakah hasil bagi
(b merupakah hasil bagi  oleh 9)
oleh 9)
Akan dibuktikan bahwa rumus benar untuk n = k + 1. Pembuktian:
kemudian  dimodifikasi dengan memasukan
dimodifikasi dengan memasukan  .
.
Contoh Soal 1
Buktikan bahwa 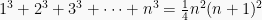
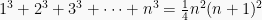
Pembahasan:

(terbukti)
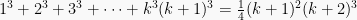
.
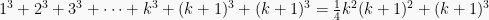
(kedua ruas ditambah

.

{terbukti).
Contoh Soal 2
Buktikan bahwa
Pembahasan:
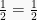
(terbukti)

Dibuktikan dengan:
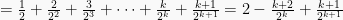
(kedua ruas dikali

)
 (2k dimodifikasi menjadi 2k+1)
(2k dimodifikasi menjadi 2k+1)

(terbukti)
Contoh Soal 3
Buktikan bahwa
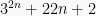
habis dibagi 5.
Pembahasan:
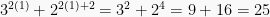
habis dibagi 5 (terbukti)

(dalam kurung dibuat sama

(

dibuat 10 dan

dibuat 5, agar bisa dibagi 5)

Tidak ada komentar:
Posting Komentar